Formule des nombres premiers
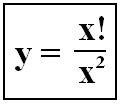
Si x est premier, alors y n’est pas entier. (Exception x=4)
Téléchargements: Brochure explicative: Grille, requiert Photoshop
Pour la grille, choisissez votre plan dans les calques: Nombre premier, factorielle ou puissance et déplacez les rêgles gauche-droite et haut-bas.
Photoshop en ligne gratuit: https://www.photopea.fr/
.
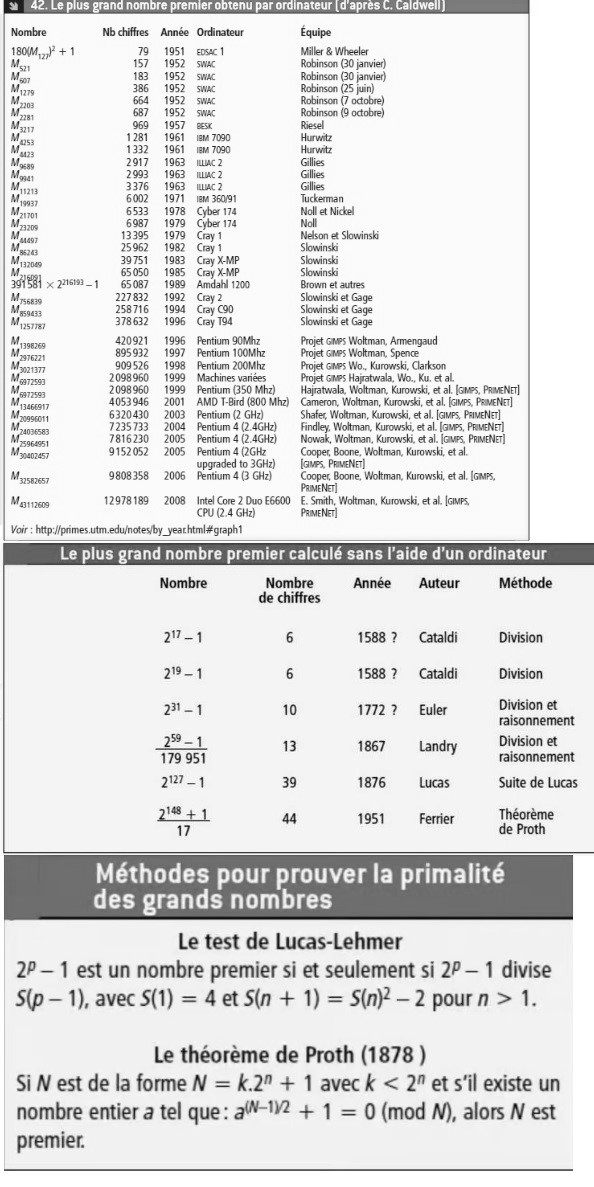
Le consulat des nombres premiers
Nombres premiers de 98 chiffres
Np = 2419 x 2³¹¹ − 1=
10091704374790393533815542006297161260203012186681138770511511033831932649733143536143643141210111
Np = 41113 x 2³⁰⁷ − 1 =
10719828492165084987488589771209569834919554568804817545267666213671254832277767936168706088894463
Depuis , le plus grand nombre premier connu est :
C’est un nombre comportant 41 024 320 chiffres. Il a été découvert le par le Great Internet Mersenne Prime Search (GIMPS) et confirmé le . Si l’on imprimait tout cela, ça serait l’équivalent d’une bibliothèque municipale.
Je peux affirmer que
est un résultat non entier, nous dépassons complètement la quantité des étoiles.
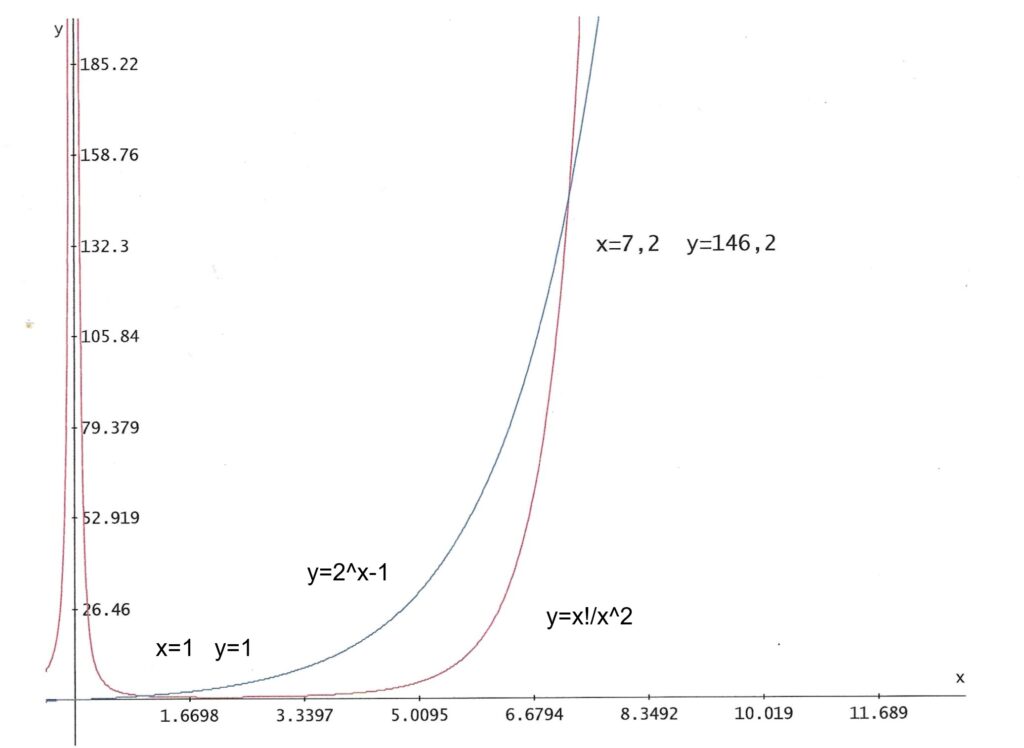
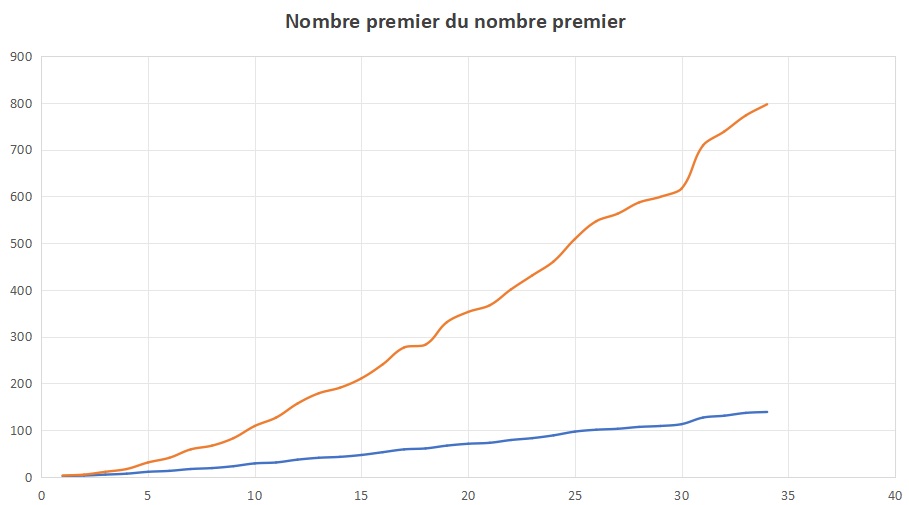
Ci-dessous, le graphique des nombres premiers, évidemment toujours sans formule simple. Voilà ce qu’on voit quand on inverse les axes. Puis les différences entre chaque nombres premiers jusqu’à 5000, il y a 162 fois un écart de 6.
On peut dire que LA FORMULE des nombres premiers est celle de Mersenne (y=2^x-1) pour trouver les plus grands, c’est celle qui est le plus utilisée. Le graphique de gauche avec ma formule y=x!/x^2 se croise deux fois (Par un et par lui-même?). Le graphique de droite, je me suis amusé à faire les nombres premiers des nombres premiers.
J’ai aussi testé la formule de Dusart qui est relativement précise:
